GeMRTOS RTOS Task Periods: Infinite Loop vs Periodic Tasks

In GeMRTOS on Altera FPGA platforms with Nios V processors, real-time tasks can be implemented as infinite-loop tasks or as periodic tasks. While infinite-loop tasks are the most common pattern in embedded RTOSs, they introduce subtle frequency perturbations that can compromise physical signal processing. This article explains both models, connects them to the Whittaker–Nyquist–Shannon sampling theorem, and shows how GeMRTOS supports both approaches concurrently within the same system.

Infinite-Loop Tasks and the Concept of Period #

In embedded RTOS operating systems, real-time tasks are typically implemented as infinite loops:

void task_code(void *pdata)
{
  while (True) {
	… task code …
    task_suspend(task_period);
  }
}

In this model, each loop cycle involves the task executing its code and then suspending itself for the duration of the task’s period. For example, a task responsible for reading sensor data would continuously read from the sensors, process it, and then suspend itself until the next cycle.

Using this task structure, the task code is not executed periodically but rather at a constant interval between the completion of one iteration and the beginning of the next. RTOSs call this suspension interval the task period, but this term does not strictly correspond to the definition in real-time terminology.

In real-time terminology, the concept of the period of a real-time task is closely related to the sampling period of Whittaker–Nyquist–Shannon‘s theorem. This theorem asserts that the information of a physical signal can be retained through periodic sampling, laying down the conditions of periodicity necessary for this preservation. Real-time tasks executed with strict periods can properly preserve and process the information of the physical signals.

If the time interval between successive executions of a task depends on its own execution time — and also on the execution time of higher-priority tasks — then the conditions of Whittaker-Nyquist-Shannon’s theorem for preserving information from the physical domain are not guaranteed. Real-time tasks implemented as infinite loops do not execute periodically and therefore put at risk the fulfillment of those conditions.

Periodic Real-Time Tasks in GeMRTOS #

GeMRTOS supports tasks implemented as infinite loops and also offers the definition of real-time tasks with periodic invocations. These real-time tasks are released at regular intervals, maintaining a consistent time gap between consecutive invocations as specified by the task period. This feature allows for the implementation of physical signal processing tasks, ensuring data integrity in accordance with the Whittaker-Nyquist-Shannon theorem.

The code for a periodic real-time task in GeMRTOS consists of a straightforward function that GeMRTOS releases at regular intervals:

void task_code(void *pdata)
{
	… task code …
}

A periodic task may experience jitter due to the execution of higher-priority tasks, but it eliminates the drift that is unavoidable in infinite-loop tasks.

Why Task Period Matters: Physical Signal Sampling #

Real-time systems engage with their surroundings through physical signals that must be sampled according to the sampling theorem to retain all information from the environment.

To apply the sampling theorem effectively, it is useful to view physical signals as combinations of sinusoidal functions — made possible by the mathematical principles of the Fourier series and transform, which assert that any function can be represented as a combination of sine and cosine waves.

The Fourier series states that a continuous periodic signal can be expressed as:

\(F(t)=\frac{a_0}{2} +\sum_{n=1}^{\infty} [a_n\cdot \cos(\frac{2\cdot \pi \cdot n}{T} \cdot t) + b_n \cdot \sin(\frac{2\cdot \pi \cdot n}{T} \cdot t)] \)
where
– \( a_0 \) is the constant coefficient,
– \( a_n \) and \( b_n \) are the coefficients of the cosine and sine terms (the Fourier coefficients), respectively,
– \( T \) is the period of the input signal,
– \( n \) is the frequency index, and
– \( t \) is the time.

All real-world signals do not require an infinity of frequencies. While some signals may require a wide range of frequencies to accurately represent them, this range is always finite for real-world signals. As a result, real-world signals can be expressed by limiting the frequency index (n) to a finite value N. This maximum frequency index N determines the bandwidth of the periodic signal and consequently the maximum frequency needed to express the signal using the Fourier series.

NOTE: Frequency response analysis offers important insights into how a system reacts to various input frequencies. Engineers can learn how a system amplifies or attenuates signals at various frequencies by examining its frequency response — essential for building filters, equalizers, and other signal processing components. It enables identification of resonant frequencies, stability problems, and other significant system characteristics.

With this in mind, Whittaker–Nyquist–Shannon‘s theorem states that a real-world signal can be sampled faithfully if it is sampled at more than twice the maximum frequency of the signal (the frequency with the N-index). The samples produced preserve all the information of the signal from the continuous-time domain to the discrete-time domain, where the information can be processed by the real-time system.

The figure below shows the various fundamental aspects involved in processing real-world signals within a real-time system.

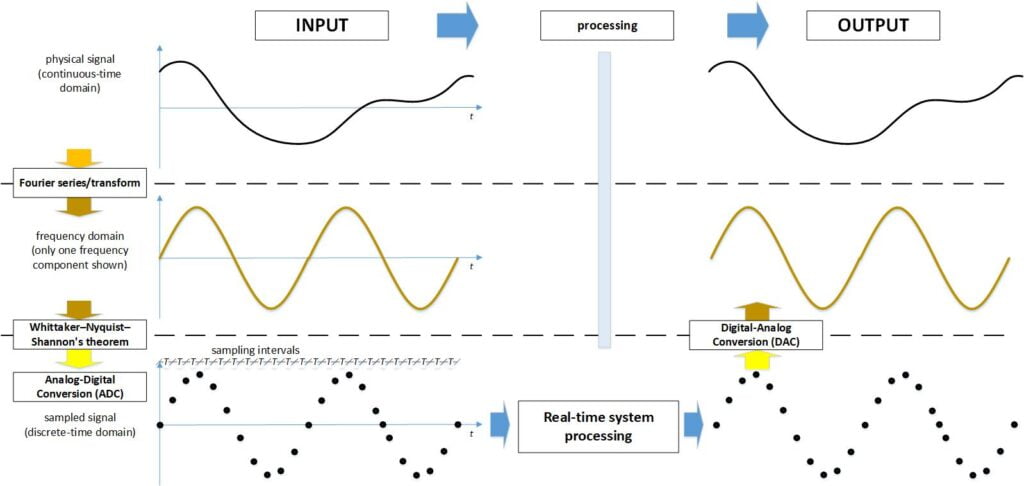
For simplicity, the real-time processing depicted in the figure merely involves copying the input value to the output value, resulting in an output signal identical to the input signal.

When the sampling interval fails to meet the conditions of the Whittaker–Nyquist–Shannon theorem, disturbances are introduced that impact the output signal. Inherently, real-time tasks executed as infinite loops do not adhere to these conditions.

To illustrate the disturbances caused by infinite-loop tasks, consider generating a sinusoidal output from a table of N pre-sampled values. If the task were executed periodically with period T, the output sinusoidal period would be:

\(Period_{sinusoidal \space signal} = N \cdot T \)

However, for an infinite-loop task with suspension time T, the actual output period also depends on each invocation’s execution time:

\(Period_{sinusoidal \space signal} = N \cdot T + \sum_{i=1}^{N} C_i\)
where:
– \( C_i \) is the execution time of invocation \( i \) of the task.

The continuous execution of the infinite-loop task therefore introduces frequency perturbations in the output signal. These perturbations vary based on the task’s execution time, potentially causing deviations from the expected frequency response of the system.

Key Takeaways #

• Most embedded RTOSs implement tasks as infinite loops suspended for a fixed interval — this balances system load but introduces frequency drift that violates the Whittaker–Nyquist–Shannon sampling theorem.
• Periodic tasks in GeMRTOS are released at true fixed intervals on Nios V FPGA, eliminating drift and guaranteeing compliance with the sampling theorem for physical signal processing applications.
• The Fourier series provides the theoretical basis: any real-world signal has a finite bandwidth, and sampling at more than twice the maximum frequency preserves all signal information in the discrete-time domain.
• Infinite-loop tasks may introduce frequency perturbations proportional to execution time — manifesting as vibration, noise, heat, or electromagnetic interference in physical applications.
• GeMRTOS supports both infinite-loop and periodic tasks concurrently — within the same scheduling list or in separate ones — enabling mixed designs where background tasks coexist with strict periodic signal-processing tasks.